How I Learned to Stop Worrying and Claim the Duke: A Design Analysis of the Game Coup

Here is an example that most people who have played Coup can relate to. I’m playing a 6-player game and I have a starting hand of a Captain and an Ambassador. I go first and use my Ambassador to look at 2 cards, I see two Dukes. I keep the Captain that I have, take a Duke, and pass the turn. The player beside me says they have a Duke and goes to take 3 coins. Right away, I’m kind of suspicious. There are only 3 Duke cards in the game, and I’ve seen 2 of them. I’ve played with this person before and I have a handle of approximately how often they decide to lie. I crunch the numbers in my head and figure, even though there is a pretty good chance he doesn't have a Duke, it's early in the game, and I still don't have much information, so I won't call them out. This same thought process goes through my mind as the next person takes their turn and claims Duke, and as the next person does the same thing. It’s impossible that all these people have Dukes, and all of them claim Duke every single game, so I am almost positive they are lying. Still, I don’t call them out, in fact, nobody at the table calls anybody out, and the game continues.

Situations like this one are very familiar to most people who have played Coup. The notion that "Everyone at the table always has a Duke" has become a running joke in my playgroup, and in many other playgroups. But why is this line of play so universal? This article will be an analysis of Coup's early game (being the first 1-2, sometimes 3 turns), exploring why everyone always claims Duke, how you can benefit from it, and why it is ultimately good for the game.

The question of why everyone always claims Duke can be broken down into three observations about the game.

First, In any kind of game, spending resources in order to preform an action that hurts a single opponent, gets more inefficient the more opponents you have in the game.

In Coup, there are many actions like this, that allow you to target a single opponent and deplete their resources. Coups and assassinations allow you to spend coins in order to take away a single player's influence, and captains allow you to use your turn action to take coins away from a player. Taking the Captain as an example, it manages to be the most powerful card in the last few turns of the game, and be one of the weakest card in the first few turns of the game for exactly this reason. When there are only two players left, being able to take away two coins from your opponent every turn is a huge advantage, and will increase your chances of winning massively, as you will be gaining resources, while keeping your only competition from gaining any. In contrast, during the beginning of a game with 5-6 players, stealing 2 coins from a player is not much different from collecting two coins from the center. Your chances of winning go up slightly since that opponent now has 2 less coins to work with, but each of your other opponents are not hurt at all. In fact, they all benefit from one of their opponents losing coins and increase their odds of winning slightly, and they didn't even have to use their turn to do so.

Second, Duke is the best action to use early game.

This one is not too hard to convince people of. It is the consensus of most players that these are the power-rankings of influence actions in the early terns of the game.

1. Duke - Allows you to stockpile on coins, which you need in order to win. Puts you in a strong position to be able to Coup or assassinate someone in the future.

2 Ambassador - Is good for much of the same reasons the Duke is, but instead of letting you stockpile coins, the Ambassador allows you to stockpile on the second most important resource in the game, information, allowing you get a better idea of what your opponents might have, and to set yourself up with cards that will be useful in the future.

3. Assassin - A very powerful action, but brought down by the fact that it is targeting a single player in a game with many players. You are using your turn and your coins to preform an action that benefits almost everyone at the table. The assassin is also lower in the rankings for the early game because it takes 3 coins to use, meaning you definitely can't use it turn 1, and won't be able to use it turn 2 without first using a Duke or foreign aid.

4. Captain - For the reasons discussed earlier, Captain isn't a great card to use in the first turns of the game. To make it worse, it can also be blocked by 2 roles, Captain and Ambassador, meaning that even if you do try and use it, it is very likely your opponent will block your action.

5. Contessa - Not terrible to have, but it does not give you any action to use, so its not really relevant to the discussion.

Third, it is not a good strategy to challenge anyone in the early game.

This claim is a bit more bold than the other two, and is going to take a bit more explaining (and math) to hash out exactly why it is the case. The crux of this argument revolves around the fact that challenging an opponent is an action in which, just like using the Captain or performing a Coup, you are spending your resources only targeting one player in a game with many players. The major difference between a challenge and the other actions of this type is that the resource you spend to challenge is not coins or even a turn action, but it is risk of losing influence. If you challenge someone, and there is a 50% chance that they are telling the truth, then you are effectively spending 50% of one of your cards in order to challenge them, as every 1 out of 2 of these challenges will result in you losing a card. This makes the payoff in the early game pretty small. In the best case scenario, one opponent will lose a card, but it will only put you a small amount closer to winning, since there are 4 other opponents in the game that didn't lose anything. On the other hand, losing a card yourself puts you a lot closer to losing. You put yourself one Coup away from being out, you lose half your options for later in the game, and the Ambassador option become much weaker.

OK, but this doesn't prove that it's always bad to call people out in the early game. Sure, when you're 50% certain they're lying, it's not a good idea to call them out on it, but what if you're 66% sure they're lying, or 75% sure, should you call them out then? We know that if you start the game with a Duke and an Ambassador, then you use the Ambassador and see two more Dukes in the deck, you should challenge your opponent's Duke because you are 100% sure they are lying. So the reward does outweigh the risk at some point, but what percentage is that going to be at? (This is where a bit of math comes in)

We can guess that percentage by estimating the payoffs for each of the strategies that player's can use during a Coup turn, then finding the Mixed-Strategy Nash Equalibrium of those payoffs.

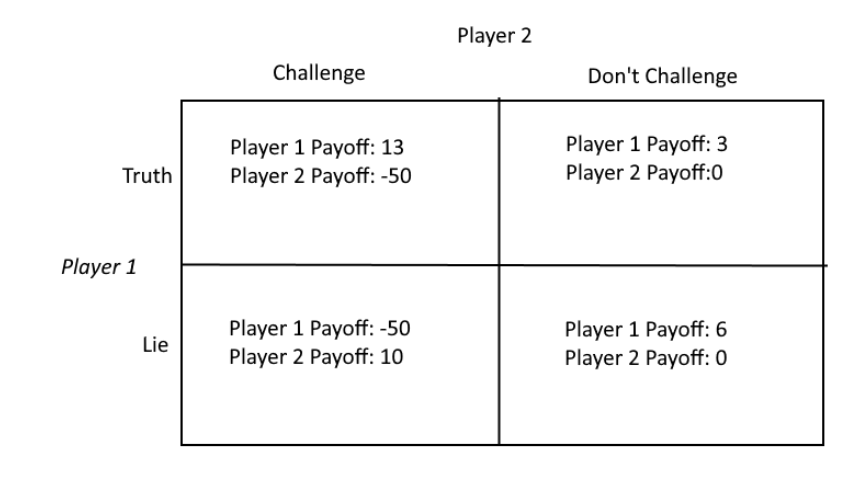
Here are my guesses for the different player's payoffs, in generalized units of utility, instead of measuring them in coins, or information, or influence.

If you've never seen a payoff matrix like this before, here's a brief explanation (if you have, skip to the next paragraph). Each player has two options that they can independently decide to make on their turn. Player 1 can choose to either lie or tell the truth, and Player 2 can either choose to challenge or not challenge. Each panel of the matrix represents one combination of these strategies. For example, the bottom left is what happens when Player 1 lies and Player 2 challenges them. Player 1's payoff in this case is negative 50 units of utility, because they lose one of their cards, putting them in a much worse situation. Player 2's payoff is positive 10 units of utility, since one of their opponents lost a card, which increases their chances of winning slightly, but not by much since this is happening in the early game. By looking at each of the other 3 scenarios and the strategies they refer to, you can understand why each player is gaining and losing utility in that case.

It is important to note that these payoff are just my estimates. They are not based on any sort of data set, just my feelings on what they might be from playing many games of Coup. So any numbers derived from the matrix should not be taken as an exact value, but rather as a starting point in some wide range of what the value should be. Mostly, this is just to show that the percentage of the time Player 1 has to lie for Player 2 to be inclined to challenge has to be very high. That being said, by calculating the Mixed Strategy Nash Equilibrium of this matrix, we get a value of 83% lie rate from Player 1 for Player 2 to be indifferent between Challenging and not Challenging.

(If you want to learn more about what a Mixed Strategy Nash Equilibrium means precisely and how it is calculated, I'd recommend checking out https://www.youtube.com/watch?v=fvEQujUcPv4. This video is a great starting point. It is episode 7 in a series that covers all the basics of Game Theory, so if you know nothing about the subject, you should probably start on episode 1 to get the best understanding).

So according to my estimates, if there is less than an 83% chance that Player 1 is lying, Player 2 should not challenge them. Then the question then becomes, does Player 1 lie at least 83% of the time.

In the matrix above, I put the payoff of telling the truth when unchallenged as 3 and the payoff to lying when unchallenged as 6. This is because on average, lying is going to give you a better result than telling the truth, but that does not mean it is always the best choice to lie if you think you can get away with it. If you have a Captain and a Contessa, telling the truth and using a Captain might give you 3 utility, but lying and using the best possible action for you at the moment, the Duke, would give you 6 utility. In the same situation, but instead of having a Captain you have a Duke, you should now just tell the truth. Collecting tax with the Duke is still going to net you the best bang for your buck when compared to all other options, so there is no reason to lie and claim an action you don't have, that is worse than the action you do have.

We can quantify this amount of time that a player’s best option will be to tell the truth. To start let's continue to assume that the Duke is in fact always the best action to use early game. The probability that an opponent will have at least 1 Duke in their opening hand, not knowing anything else about any other cards, is 37%. If you look at your hand and you do not have a Duke, that number goes up to 42%, and if you do have a Duke in your hand, the probability that the opponent also has one becomes 29%. If we use the example from the beginning of this article, where I used the Ambassador and found the location of 2 of the Dukes, the probability goes all the way down to 18% that my opponent has a Duke. So, if this opponent plays the time-tested strategy of always claiming Duke every time no matter what, and takes 3 coins on their turn, then we can get the probability that they do not have a Duke, and hence the probability that they are lying, by simply taking the inverse of the probability that they do have a Duke, so 63%, 58%, 71%, and 82% respectively for the 4 situations above. All these are below 83%, meaning that it would not be good to challenge the opponent even if they claimed Duke every single time.

Two caveats to that. First off, the 83% number is an estimate. So 82% is way to close to be sure that it’s still bad to challenge. Secondly, I made an observation earlier that Duke is always going to be the best action early game, which I think is probably true, or at least usually true, but I'm sure that some people reading this who have played a lot of Coup are currently thinking that there is an argument to made for other cards. To address the first problem, it takes a very specific scenario for this 82% certainty to come up, so it will be very rare, and there is an argument to be made that if the opponent you’re suspicious about claims Duke every single time and this situation comes up, then you might want to challenge them. But again, it is not going to come up very often, as you need to be able to know the location of 2 of the 3 Dukes. On the other hand, if you are the liar and you want to be able to play around this scenario, however rare it might be, we can actually do that by addressing caveat number 2. The claim that Duke is the best call every single time could very well be accurate, it’s hard to know for sure, but I’d say the only card that could compete with Duke for that slot is Ambassador (This goes back to reasoning made earlier in the power ranking paragraph). Without any data it is hard to tell which is for sure better, and how much better one is than the other (if anyone out there has a Coup data set please let me know, I'd love to see it). But I think it’s safe to say that they are pretty close in power level. Since this is the case, it might be a good strategy when lying, to call Ambassador sometimes in the early game instead of Duke, and do it in such a way so that when you actually have an Ambassador in your hand, you call Ambassador slightly more often than you would otherwise. The same when you have a Duke in your hand, you call Duke slightly more often. This way, even if you think Duke is always going to be a better action that Ambassador, by sometimes losing the little bit a value you would get by calling Duke instead of Ambassador, you lower the probability to others that you are lying. Even if your opponent has great information, you make it so a situation where having enough information to reasonably call you out if almost guaranteed to not happen.

OK, cool, but where are you going with all this?

With these three observations, we can conclude that when everyone is always claiming Duke in the first few turns, it is not going to be a good idea to call them out, because the threshold of certainty your need to justify challenging is so high , and because some inevitable amount of the time, a player happens to have the card they were going to claim anyways. This makes it so you are never sure enough that they don't have it to take the risk of challenging.

Now is where I explain why I think that even though everyone constantly claiming Duke makes the first few turns of the game the same, and even a little boring, it is ultimately good for the game.

I think that by making lying in the early game much easier to get away with, Coup manages to counter-balance the randomness of the cards dealt at the start of the game. All the cards in the game are balanced overall, but there are some cards that are better early game, and some cards that are better late game. For any game that involves chance, if you are playing with experienced players, who are familiar with the strategies that allow you to play a “near perfect” game, these chance elements could be enough to swing the game in someone’s favor. In Coup, players can get around being dealt sub-optimal cards because they can just lie about what they have. Still, lying about having a card is not going to be as good, on average, as if you actually had that card in your hand, since you are risking getting challenged. If a player gets N units of utility from using an action, we can say that the average amount of utility they will get from lying about the same action will be N*(the chance that they will go unchallenged). But, as we just found, the early game is designed in such a way that challenging almost never happens, since it is very disadvantageous for the challenger, so that percentage is very high. This means that using a card that you have and using a card that you don’t have are almost identical in their probable outcomes. This actually balances out the random element in the game a lot. The person who uses the Duke that they actually have on turn one, is only in a slightly more favorable position than the person who bluffs a Duke turn 1, giving players who have a bad hand a few turns to gain their footing, and get to a more comfortable position without risking too much, creating a game that is much more balanced and skill-intensive at high levels, rather than relying on more luck the more skilled your playgroup is.

This whole thing opens up a lot more interesting questions in Coup strategy, such as, “would I rather start the game without a Duke in hand, since early game bluffing Duke is just as good as having Duke, and late game, actually having a Captain or Assassin is a lot better than bluffing one?” I think the answer might be yes… but that is probably a question for another article.